[架構配置入力]▶〔節点・部材〕▶[面要素]▶[面要素のグリッドシート入力]
面要素を配置します。
面要素は面内応力、面外応力を扱う平面板要素です。
下記の分割タイプ、分割数、補正レベルから自動分割した三角形要素の集まりとみなします。
応力計算に用いる面要素の剛性は、境界節点以外の分割点の自由度を縮約消去して作成します。

面要素は面内応力、面外応力を扱う平面板要素です。
下記の分割タイプ、分割数、補正レベルから自動分割した三角形要素の集まりとみなします。
応力計算に用いる面要素の剛性は、境界節点以外の分割点の自由度を縮約消去して作成します。
 |
グリッドシート |
 |
テキスト形式 |
 |
説明 |
 グリッドシート
グリッドシート

①名称
15文字以内で入力します。
②材質
- 種別
- 「0:RC/SRC」、「1:S」、「2:木」、「3:その他」から選択します。
- コンクリート
- [種別]が「0:RC/SRC」の場合、【コンクリート材質】で定義した名称を入力します。
- 鉄骨
- [種別]が「1:S」の場合、【鉄骨材質】で定義した名称を入力します。
- 木
- [種別]が「2:木」の場合、【木材質】で定義した名称を入力します。
- 材料
- 【材料】 で定義した材料名称を入力します。
[種別]が「3:その他」以外の場合、【応力準備計算】で自動生成します。
[種別]が「3:その他」の場合、直接入力します。
③厚さ
面要素の板厚を入力します。
④剛性
「0:面内」、「1:面内+面外」から選択します。
⑤分割
- タイプ
- 「0:グリッド分割」、「1:フラクタル分割」、「2:図心分割」から選択します(詳細は、
 説明6.を参照)。
説明6.を参照)。 - 数
- 0~20までの分割数を入力します。
- 補正レベル
- 「0(補正なし)」、「1(弱)」、「2(中)」、「3(強)」から選択します。
境界節点、境界上の分割点を除く面要素内の分割点をラプラシアン法で補正します。
⑥境界節点
【節点】で定義した節点名称を入力します。
面要素を配置する境界上の節点を、時計回りまたは反時計回りに入力します(最大30節点)。
面要素を配置する境界上の節点を、時計回りまたは反時計回りに入力します(最大30節点)。
 テキスト形式
テキスト形式
| 項 目 | 省略値 |
|---|---|
| 名称 | |
| 材質-種別 | 0 |
| 材質-コンクリート | |
| 材質-材質 | |
| 材質-木 | |
| 材質-材料 | |
| 厚さ | 0.0 |
| 剛性 | 0 |
| 分割-タイプ | 0 |
| 分割-数 | 0 |
| 分割-レベル | 0 |
| 境界節点-1 | |
| 境界節点-2 | |
| 境界節点-3 | |
| 境界節点-4 | |
| 境界節点-5 | |
| 境界節点-6 | |
| 境界節点-7 | |
| 境界節点-8 | |
| 境界節点-9 | |
| 境界節点-10 | |
| 境界節点-11 | |
| 境界節点-12 | |
| 境界節点-13 | |
| 境界節点-14 | |
| 境界節点-15 | |
| 境界節点-16 | |
| 境界節点-17 | |
| 境界節点-18 | |
| 境界節点-19 | |
| 境界節点-20 | |
| 境界節点-21 | |
| 境界節点-22 | |
| 境界節点-23 | |
| 境界節点-24 | |
| 境界節点-25 | |
| 境界節点-26 | |
| 境界節点-27 | |
| 境界節点-28 | |
| 境界節点-29 | |
| 境界節点-30 |
 説明
説明
- 構造形式により、次の項目が入力可能です。
項 目 平面フレーム 平面トラス 平面格子ばり 立体トラス 立体フレーム 剛性 〇 - 入力補助ツール
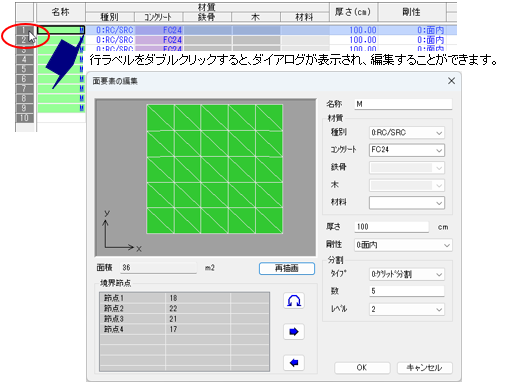
グリッドシートの行ラベルをダブルクリックすると、ダイアログが表示されます。
各項目を設定し、[OK]ボタンをクリックすると、 グリッドシートの各項目が更新されます。


: 境界節点の順番が逆になります。 

: 境界節点の順番が1つ後ろへずれます。最後尾の節点は節点1へ移動します。 

: 境界節点の順番が1つ前へずれます。節点1は最後尾へ移動します。 

: 境界節点の順番が1つ前へずれます。節点1は最後尾へ移動します。 - 面要素を4つ以上の境界節点に配置する場合、同一平面上に定義された節点に、凸多角形になるように配置する必要があります。
- 隣りあう節点の間には、はり、柱、トラスが配置されている必要があります。
- 分割は、三角形要素が1000要素未満になるように分割タイプ、 分割数を設定する必要があります。
- 分割タイプにより、次のように分割します。
 グリッド分割
グリッド分割① 面座標系でx方向長さLx、y方向長さLy、分割数nとします。 ② 長辺方向の長さを分割数nで除した長さをグリッド間隔としたグリッドを作成し (下図の場合グリッド間隔Lx/n)、 グリッドの交点とグリッドと境界線上の交点を分割点とします。

③ 境界上の分割点を等間隔に配置します。 ④ 作成された分割点に対し、Delaunay三角形分割を行います。

 フラクタル分割
フラクタル分割① 面要素の分割数をnとします。 ② 境界節点に対しDelaunay三角形分割を行います。

③ 作成された三角形の各辺をn分割した点を利用し相似な三角形を作成します(左下図は1-2-4三角形を2分割した例)。 ④ ②で作成した各三角形について③の分割を行った各交点を分割点とします。

 図心分割
図心分割① 面要素の図心位置を求めます。 ② 境界節点と図心位置に対しDelaunay三角形分割を行います。

③ 作成された三角形の各辺をn分割した点を利用し相似な三角形を作成します(左下図は1-2-4三角形を2分割した例)。 ④ ②で作成した各三角形について③の分割を行った各交点を分割点とします。

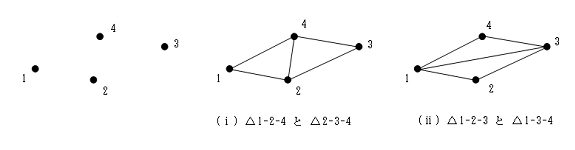
- Delaunay三角形分割とは、平面上に任意に設定された点を対象としてそれら点の支配する領域を三角形集合で隙間無く覆う一つの手法です。
最大の特徴は、Delaunay三角形分割してできあがった三角形の外接円内の中には他のいずれの点も含まれていないことです。
下図のように4つの節点を考えた場合、2種類の三角形分割が考えられますが、 Delaunay三角形分割は、(ⅰ)のように対角線が短くなるような三角形分割を行います。
- ラプラシアン法は形状修正を行う1つの方法で、次式で示される位置に節点を移動します。
$$\mathrm{P(i)=\frac{1}{2n}\sum^{n}\{P(j)+P(k)\}}$$i (移動点),j,k : 1個の三角形の頂点 P(i),P(j),P(k) : 各頂点の座標値 n : iを共有する三角形の個数 
▲PAGETOP